Intro to Content-Defined Chunking

Published on to joshleeb's blog

This post is the first in a series on Content-Defined Chunking (CDC) where we’ll explore Gear-based chunking techniques. After this intro, we’ll look at implementing a chunking algorithm using Gear Hashing, before exploring significant improvements from the FastCDC, and then the RapidCDC and QuickCDC papers.

But before all that… What is Content-Defined Chunking, and what is it used for?

Intro to Chunking

Chunking is the process of splitting a file, or more generally a sequence of bytes, into contiguous regions called chunks.

Working with chunks makes it trivial to stream a file from disk by reading in a chunk at a time. And it improves the chances of success when sending large files over a faulty network by reducing the amount of data we have to resend (one chunk, not the whole file) if something gets corrupted during transfer.

However the use case I’m most interested in is deduplication.

When we chunk a file, we have to have some way of putting it back together. We can do this with some kind of index that maps the file to an ordered sequence of chunks. With this, duplicating the file doesn’t duplicate its contents (i.e: the chunks). Rather, we just duplicate the index which is assumed to be much less data than the file itself.

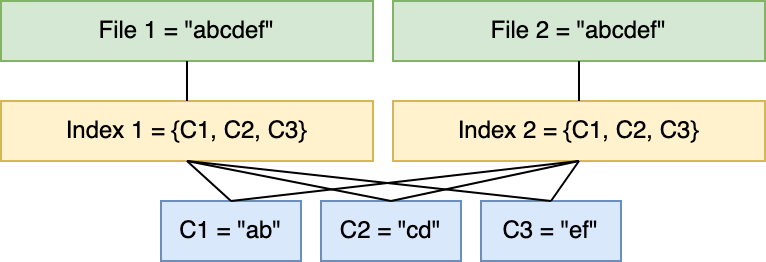
Taking this property a little further, it’s not just whole files that can be deduplicated but the chunks themselves. To illustrate this we’ll use the example of a git repository.

Each commit represents changes being made to the source tree. Most of the time these aren’t large changes replacing whole files, they’re much smaller modifications to a few lines here, and a few lines there. So it seems wasteful to store a distinct, full copy of the source tree for every commit.

Instead, if we chunk each file then we don’t have to duplicate the chunks that make up files with no modifications. But even files that are modified, we can deduplicate all the regions that are unchanged. It’s only the changed regions that will produce new chunks to be referenced in the index for that version of the source tree.

If you’re familiar with persistent data structures, specifically those with structural sharing as used in Clojure, then the concept is quite similar.

Now that we’ve established what chunking is, and why it is useful, let’s take a high level look at how to chunk files. We’ll start with the naive approach, fixed-size chunking.

Fixed-Size Chunking (FSC)

FSC is the simplest form of chunking. We take a sequence of bytes and split it up into fixed-size chunks. The implementation is trivial.

#[derive(Debug, Clone, PartialEq, Eq)]
struct Chunk {
    pub offset: usize,
    pub len: usize,
}

// Naive implementation of fixed-size chunking producing chunks of size
// `desired_len`.  Could be // better implemented with `Iterator::step_by`
// or `Iterator::chunks`.
fn chunk(bytes: &[u8], desired_len: usize) -> Vec<Chunk> {
    let mut chunks = vec![];
    let mut index = 0;
    while index < bytes.len() {
        let len = std::cmp::min(desired_len, bytes.len() - index);
        chunks.push(Chunk { offset: index, len });
        index += len;
    }
    chunks
}

Along with simplicity, this approach is also fast, and it produces evenly sized chunks which we’ll see is not guaranteed by all chunking strategies. But there is one major drawback which is the deduplication ratio.

Let’s go back to our git example. And say you’re modifying a file by adding a character at the start of the file. Now the offset of all subsequent bytes has changed, but FSC can’t shift the chunking boundary. It doesn’t know that the modification made was adding a single character. All it can do is produce chunks at evenly spaced offsets.

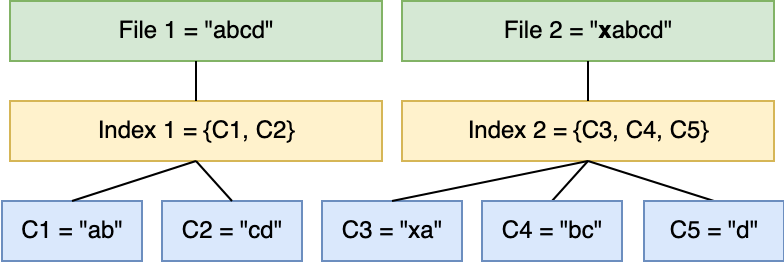
In the FastCDC paper [1], which we’ll take a detailed look at later in the series, this is known as the boundary-shift problem. The LBFS paper [2] also has a discussion of the issue.

To get around this drawback, we’ll have to look at a form of variable-sized chunking called Content-Defined Chunking.

Content-Defined Chunking (CDC)

CDC strategies determine chunking boundaries based on the content. This is done by looking for patterns in the byte sequence, most commonly identified with a rolling hash function.

Rolling hashes are produced by moving a window through the sequence of bytes and hashing the contents of the window. One of the key benefits of rolling hashes is their speed [3]. When the window is shifted we don’t have to produce an entirely new digest from scratch. Rather, the byte that exited the window is ‘subtracted’ from the hash, and the byte that entered the window is ‘added’ to the hash.

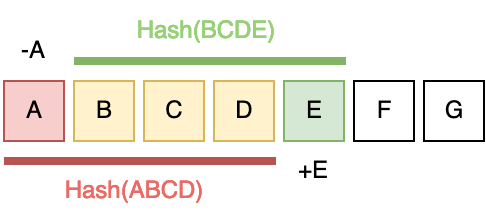
Once we have the digest, sometimes referred to as a fingerprint [3], we run a comparison to check for a chunk boundary. The comparison function is referred to in some papers as the hash judgment function [1][4].

As a result of chunking by content patterns, it is unlikely to end up with perfectly uniform chunks. CDC is also more expensive than FSC as we must compute a hash for each byte and then run the hash judgment function. But we will end up with a higher deduplication ratio by avoiding the boundary-shift problem.

In theory, any hash function can be used to run CDC. However a good hash function must have a uniform distribution of digests regardless of the input, and for this use case it must also be fast. For this reason rolling hashes make a great fit for CDCs.

The most common CDC strategies appear to fall into two categories distinguished by the kind of rolling hash being used.

First, there are the polynomial-based CDCs. These are algorithms that distribute the sequence of bytes as coefficients in a polynomial of some degree k.

Then there are the gear-based CDCs, which is where the majority of this series will be focusing. These rely on a form of rolling hash called a Gear Hash.

Comparing Chunking Approaches

Chunking approaches can be compared across three dimensions [1].

  1. size of the chunks produced, usually as a measure of the average chunk size;
  2. chunking performance, in how long it takes to run; and
  3. deduplication ratio, as how much of the original data is deduplicated after each modification.

Each of these are linked in one way or another. For example, smaller chunks might result in a higher deduplication ratio but at the cost of chunking performance. And, at the extreme end with FSC we will get very high performance and uniform chunk sizes but to the detriment of the deduplication ratio.

According to the results in the FastCDC [1], RapidCDC [7], and QuickCDC [4] papers, the optimized gear-based approaches are orders of magnitude faster than Rabin Chunking while still resulting in a similar deduplication ratio and uniformity of chunk sizes.

Wrapping Up

That’s all for this post. For the next part of the series we’ll take a more in-depth look at Gear Hashing and discuss its benefits and drawbacks. Following that we’ll see how FastCDC improved on Gear Hashing with more uniform chunk sizes, and a higher deduplication ratio.

References

  1. FastCDC: A Fast and Efficient Content-Defined Chunking Approach for Data Deduplication. Wen X., et al. (2016)
  2. The LBFS Structure and Recognition of Interval Graphs. Corneil, D., et al. (2010)
  3. Rolling hash - Wikipedia
  4. QuickCDC: A Quick Content-Defined Chunking Algorithm Based on Jumping and Dynamically Adjusting Mask Bits. Xu, Z., & Zhang, W. (2021)
  5. Fingerprinting by Random Polynomials. Rabin, M. (1981)
  6. Ddelta: A Deduplication-Inspired Fast Delta Compression Approach. Wen, X. et al. (2014)
  7. RapidCDC: Leveraging Duplicate Locality to Accelerate Chunking in CDC-based Deduplication Systems. Ni, F., & Jiang, S. (2019)