Improving on Gear Hashing with FastCDC

Published on 2023-07-04 to joshleeb's blog

In the last post we took a look at Gear Hashing for Content-Defined Chunking (CDC), and outlined some problems we noticed when analyzing the distribution of generated chunks, namely the lack of uniformity in the chunk sizes, and that a large portion of chunks were much smaller than our desired chunk size.

In this post, we’ll go through the FastCDC paper [1] which proposes a number of optimizations over Gear-based CDC to achieve a 3x improvement in chunking times while maintaining a deduplication ratio that is on-par with Rabin-based chunking methods.

At it’s core, FastCDC still uses the Gear rolling hash function and so it is categorized as a Gear-based CDC algorithm. However it is able to achieve much better results than Gear Hashing alone.

The FastCDC paper [1] proposes three optimizations that provide significant benefits.

1. An enhanced hash judgment phase;
2. Sub-minimum chunk cut-point skipping; and
3. Normalized chunking.

These sounds pretty fancy and complex, but they’re really quite simple. And each one adds only a few lines of code (if that). If you want to jump ahead and compare implementations of Gear Hashing to FastCDC, you can find my repos hosted on Sourcehut for gearhash and fastcdc.

Enhancing the Hash Judgement Phase

The first optimization proposed in the paper is to enhance the hash judgement function. This is done by expanding the sliding window used to determine the chunk boundary, and subsequently expanding the mask by padding with zero bits.

Recall from the last post that the mask is determined by the desired chunk size. Specifically that for a chunk size of M bytes, we will generate a mask with log2(M) effective bits. That is, to get an average chunk size of around 4KiB, we’ll use a mask with 12 1-bits: 0b1111_1111_1111.

The problem we have observed with a small sliding window (and mask) is that the smaller the window, the higher the likelihood of finding a chunking boundary. This explains why in the (very brief) analysis we did of Gear-based CDC we found a large volume of chunks below the desired chunk length, with many only being a few bytes.

FastCDC instead uses a padded mask. So, rather than having a mask 12 1-bits we instead have a 48-bit mask (the same size as Rabin-based CDC) and evenly distribute the 12 effective bits throughout.

mask = 1001_0001_0001_0001_0001_0001_0001_0001_0001_0001_0001_0000

You might be wondering why we evenly distribute the effective bits, instead of grouping them all together or selecting random positions. And there are two reasons for this.

1. Masks must be deterministically generated. Generating a new, random mask for every run of the CDC will mean our hash judgement function will be different for each run, and that will be extremely harmful to the deduplication ratio.
2. The FastCDC paper [1] recommends that evenly distributing the effective bits leads to a slightly higher deduplication ratio at larger scales.

On its own, this makes FastCDC very competitive with Rabin-based CDC on deduplication ratio, while blowing it out of the water with a 5x improvement in chunking speed. But the paper goes even further.

Applying Sub-Minimum Cut-Point Skipping

Now Gear Hashing is very efficient, perhaps the most efficient rolling hash known at the moment. So this next optimization comes from the observation that with Gear-based CDCs the bottleneck is no longer with generating the fingerprint. It has instead shifted to the hash judgement phase.

Given the bottleneck now lies with checking if we have found a chunk boundary, the paper proposes skipping the hash judgement phase if the prospective chunk is below a minimum size.

Fairly simple, and the FastCDC analysis suggests that cut-point skipping not only achieves a higher chunking speed, but also moves the average chunk size closer to the desired length. However this comes at the cost of the deduplication ratio, decreasing it by as much as 15% in some cases.

Chunking with a Normalization Strategy

The final improvement aims to win back the decreased deduplication ratio experienced with cut-point skipping, while also maintaining the increased chunking speed. The proposal: to adjust the chunk size distribution such that it is normalized to a specific region.

Again, this sounds fancy but lets run through it step by step.

Recall in the last post (without normalized chunking) our chunk-size distribution had a similar shape to the distribution in Figure 1.

That is, the larger the chunk size, the lower the volume of chunks produced into a long tail where some of the chunks are many times the desired length.

Normalized chunking aims to shift the shape of this graph so that it follows more of a normal distribution where the center (or the mean) is the desired chunk size, as shown in Figure 2.

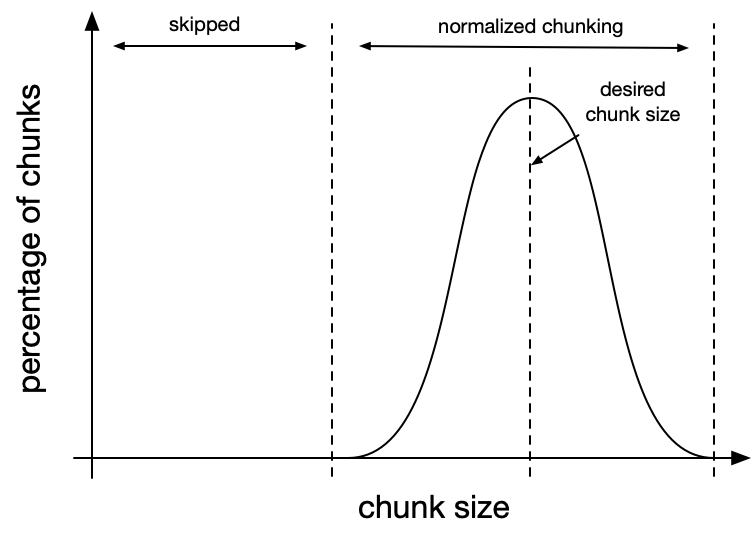
Achieving a Normalized Chunk-Size Distribution

It’s not entirely obvious how to achieve this, and so the paper proposes uses two masks instead of one in the hash judgement phase. Then, depending on the size of the prospective chunk (i.e: how many bytes we have consumed without finding a chunk boundary) we will decide to use one mask or the other.

The two masks are called the small mask (i.e: mask_s) and the large mask (i.e: mask_l), to be used (respectively) when the size of the prospective chunk is smaller or larger than the desired chunk size.

An important detail to making this work is the relationship between these two masks. mask_s must have more effective bits than mask_l, the impact of which is that with mask_s it will be harder to find a chunk boundary as it is less likely the gear hash will match the larger number of effective bits.

Conversely, mask_l must have less effective bits than mask_s, making it easier to find a chunk boundary.

By using mask_s when we has a prospective chunk that’s smaller than desired size, we are reducing the probability we will find a chunk boundary, and encouraging more bytes to go into this next chunk. But when we have surpassed the desired chunk size and we haven’t found a binary, we switch to using mask_l and biasing towards finding a chunk boundary.

The implementation of comes down to a simple if-statement to do the mask selection. We then pass the selected mask into the hash judgement function as we did with Gear Hashing.

let m = if len < desired_len { mask_s } else { mask_l };
if hasher.is_chunk_boundary(m) {
  // We have found a chunk boundary!!
}
// Continue iterating through the bytes.

Normalization Level

Now we’ve already seen how to generate a single mask given a desired chunk length. We’ll call this mask mask_d. But how should we go about generating the two masks for normalized chunking?

For FastCDC, the proposal is to adjust the masks by equal steps away from mask_d, with mask_s increasing and mask_l decreasing in the number of effective bits. Each step corresponds to a single 1-bit that is either added or removed, and the amount of steps taken is called the normalization level.

For example, let’s say we have a desired chunk length of 4KiB, and a normalization level of 2.

• log2(4096) = 12, so mask_d has 12 effective bits; then
• We set mask_s to have 12 + 2 = 14 effective bits; and
• We set mask_l to have 12 - 2 = 10 effective bits.

Figure 9 in the FastCDC paper [1] shows what shape of chunk-size distribution to expect, with their analysis using a desired chunk size of 8KiB with various normalization levels.

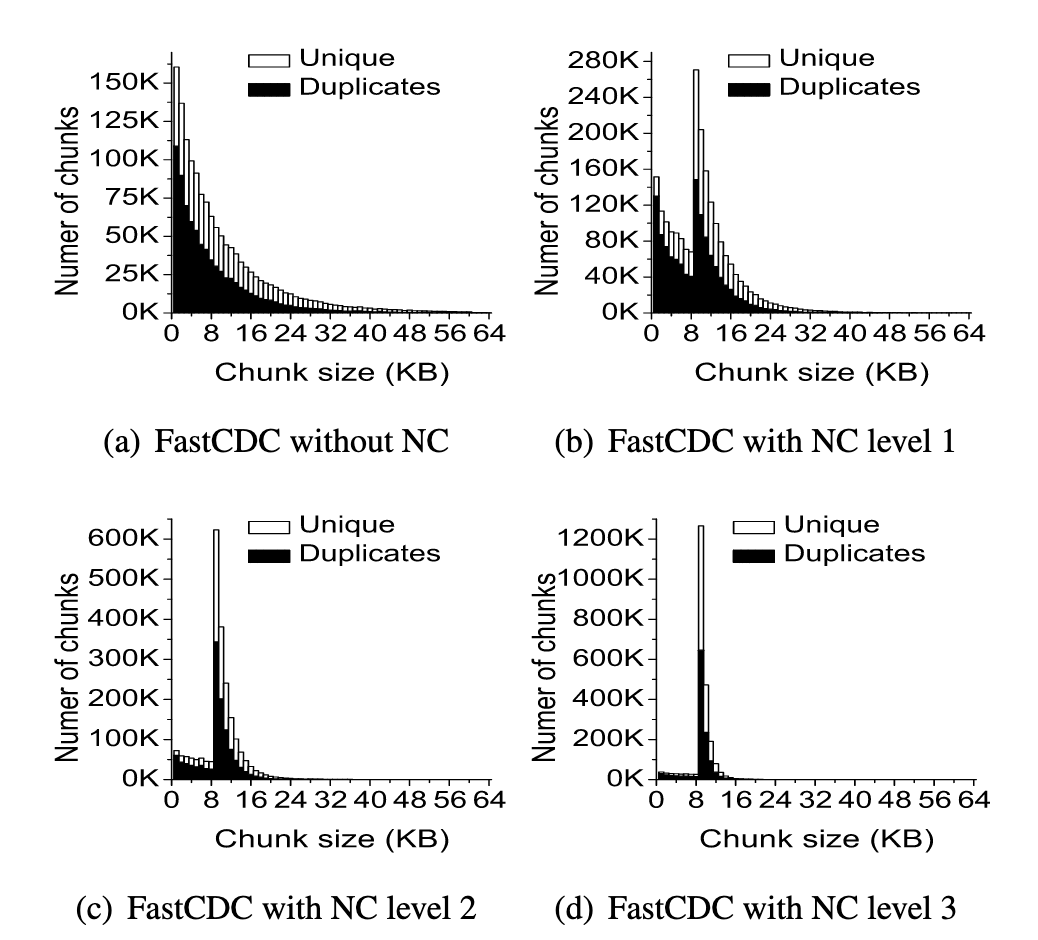
We can see from Figure 3 that a normalization level of 2 or 3 results in a chunk-size distribution that becomes a reasonably close approximation of a normal distribution centered around the desired chunk size.

Wrapping Up

The analysis in the FastCDC paper [1] concludes that FastCDC is around 10x faster than Rabin-based CDC, and around 3x faster than the unoptimized Gear-based approach we covered in the last post. And with this massive speed up, the deduplication ratio is nearly the same as Rabin-based CDC… A pretty incredible achievement!

In the next, and final, part of this series we’ll look at the papers that introduce RapidCDC (2019) and QuickCDC (2021). These chunking strategies build on the work of Gear Hashing and FastCDC to achieve even more improvements in chunking performance.

References

1. FastCDC: A Fast and Efficient Content-Defined Chunking Approach for Data Deduplication. Wen X., et al. (2016)