A Look at RapidCDC and QuickCDC

Published on 2023-08-06 to joshleeb's blog

This is the fourth and final post for the CDC series. If you’re just joining us, and would like to know more, jump on back to the first post which provides an Intro to Content-Defined-Chunking.

In this post, we’ll be concluding our exploration of CDC strategies by looking at two recently developed algorithms that bring with them some interesting techniques for speeding up CDC. First will be RapidCDC, with the paper [1] published in 2019, and then we’ll jump into QuickCDC, published [2] in 2021.

But first, a quick recap of the journey so far.

1. Prior to Gear-based CDC, Rabin Chunking was the most popular approach. When Gear was introduced, it was 3x faster than Rabin but had a poor deduplication ratio. This stemmed from the size of the chunks that were produced which, even though they averaged out to be close to the desired chunk size, were actually all over the place.
2. FastCDC was developed as a series of extensions to Gear that improve performance and the deduplication ratio. In particular: normalized chunking, sub-minimum cut-point skipping, and padding the Gear mask. FastCDC showed to be 3x faster than Gear, and 10x faster than Rabin.

Now, with FastCDC, we have a chunking strategy that is 10x faster than the previous standard, and it has a deduplication ratio that is just as good.

So where do we go to next?

Notice that neither Gear, nor FastCDC know anything about whether a chunk is duplicated or unique. All these algorithms do is tell you where the chunk boundaries are for the given data stream. Once we have the chunk boundary, then it’s up to a cryptographic hash to determine whether we’ve got a chunk that we’ve seen before.

But cryptographic hashes are expensive. So if our algorithm can determine whether a chunk is a duplicate, without using a cryptographic hash then we:

1. side-step the performance hit of using a cryptographic hash;
2. get an additional boost for duplicate chunks, where we completely skip past them.

These benefits result in not having to read every byte in the data stream through the chunking algorithm, and that’s exactly what RapidCDC and QuickCDC aim to achieve, but with some risks.

The main contribution of both papers is the suggestion to store additional data along with the chunks to provide hints for where the next chunk boundary could be. This metadata is then used to facilitate various skipping techniques, which rely on heuristics to determine whether the guessed chunk boundary is actually a chunk boundary, and whether the chunk is a duplicate, or unique.

RapidCDC

The RapidCDC paper [1] starts by introducing the concept of duplicate locality, which is where duplicate chunks are likely to appear together in data. To exploit this, the chunk fingerprint is recorded along with the size of the next chunk, which acts as a hint for where the next chunk boundary will be.

Duplicate locality is a rather intuitive phenomenon. When we update a file or some data, we do so at a particular offset. And there is a tendency that the file contents around that offset are more likely to be updated as well. Put another way, updates are unlikely to be evenly distributed in a dataset, and inversely unchanged data is likely to be contiguously laid out in a file.

Now a chunk duplicated in a dataset isn’t limited to being duplicated only once. So storing the size of just one proceeding chunk is probably not going to be that useful.

Instead, RapidCDC maintains a list of chunk sizes, in the order in which they appear. Each entry inserted using a Least Recently Used (LRU) policy, where the entry is the difference between the chunk’s size and the minimum chunk size.

Accepting Chunk Boundary Hints

Once we’ve jumped forward using the size hint from the previous chunk’s list, we need a way to verify that a hint actually matches the chunk boundary.

There are a number of options presented in §3.2 of the paper [1]. Each one take a different position on the tradeoff between the performance gain if the guess is correct, and the performance penalty if it is not.

On one extreme we have the Fast-Forwarding Only (FF) option, which always accepts the chunk boundary without running further checks at the file offset. This is clearly a very aggressive approach for fast chunking, and it can result in degrading the deduplication ratio by choosing boundaries that produce unique chunks.

On the other end, we can jump to the suggested offset, compare bytes in a rolling window with the expected bytes at the offset, and compute the fingerprint for the chunk. If these two tests pass, then the chunk is confirmed to be a duplicate. But if the chunk is unique and these tests fail then there is a relatively high performance penalty for this extra work.

Trying All the Boundary Hints

Given the list of size hints for a chunk is an ordered list, if the first size hint is not accepted as the next chunk, we’ll keep trying with the next hint in the list. Only when we have exhausted this list and not found accepted a chunk boundary will we move the window back to where the last chunk boundary was found, skip forward the minimum chunk size, and proceed to find the next chunk as normal.

In §6 of the paper [1] RapidCDC is claimed to provide up to a 33x speedup in chunking. From looking at the data, specifically Figure 13, this improvement occurred with the NodeJS dataset when compared against a standard Rabin chunking approach, and using the fastest of the boundary hint acceptance criteria.

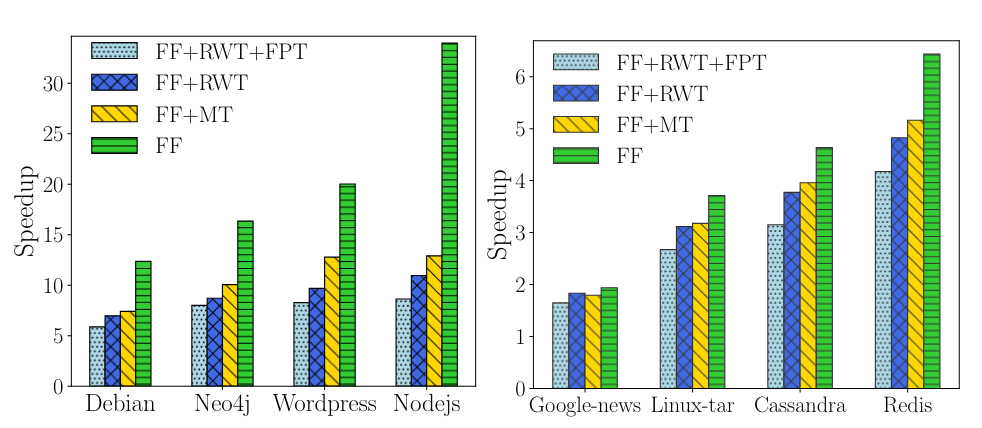
The paper [1] also considers the speedup of a Gear-based variant of RapidCDC, however results are only shown for synthetic datasets.

Considering that Gear is 3x faster than Rabin, and RapidCDC is 33x faster than Rabin, we can infer that RapidCDC is 11x faster than Gear which puts it in a similar ballpark to FastCDC.

FastCDC’s speedup mostly comes from a similar, but more naive skipping technique where we move forward the minimum chunk size after every chunk boundary. So this slight increase in performance of RapidCDC isn’t surprising.

However, what remains to be seen is the benefit from combining FastCDC’s techniques with the chunk hints introduced with RapidCDC. Which is a great segway into QuickCDC!

QuickCDC

The QuickCDC paper [2] outlines some very similar improvements to what we’ve seen already with FastCDC and RapidCDC.

1. Recording hints to subsequent chunk boundaries, which is very similar to what we just saw with RapidCDC
2. Skipping forward by the minimum chunk length, introduced by the FastCDC paper [3] as sub-minimum cut-point skipping
3. Adjusting mask bits to normalize the size distribution of chunks, which sounds very similar to FastCDC’s normalized chunking technique

The main contribution appears to be in related to (1). RapidCDC exploits the notion of duplicate locality, which means that if there is no duplicate locality then its performance degrade significantly. However, QuickCDC does not rely on duplicate locality for achieving its speedup.

The paper [2] also claims that the chunking speed of QuickCDC is 11.4x RapidCDC (the Rabin variant) and the deduplication ratio is significantly improved as well, up to 2.2x in some cases.

Skipping Strategy

To skip over duplicate chunks, QuickCDC keeps track of the chunk size, along with two features vectors which are used to distinguish between chunks. These vectors are the first N and the last M bytes of the chunks, called the front and end feature vectors respectively.

The paper [2] suggests that setting N = M = 3 is sufficient so that the probability of two chunks being the same if the front and end feature vectors are the same is 99.98%, while not consuming too much additional memory.

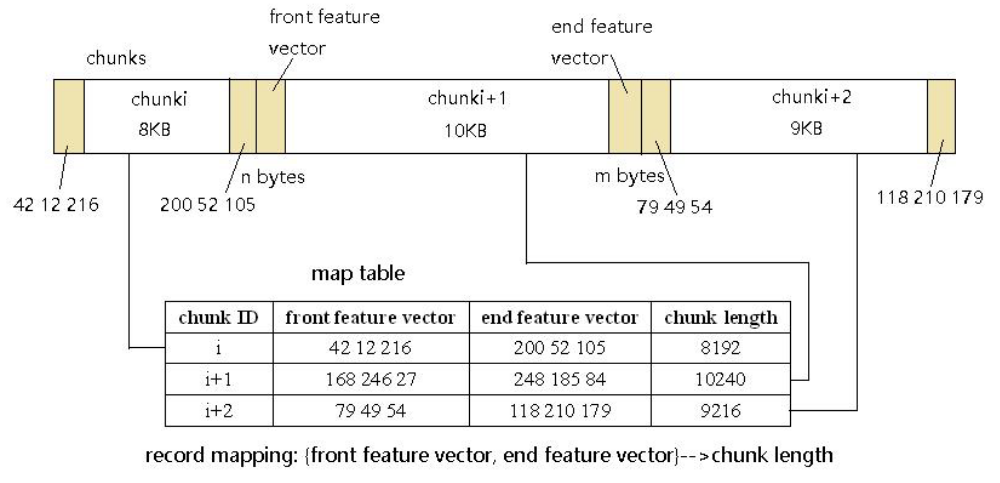
Using feature vectors allows us to quickly compare whether the chunk could be one we’ve seen before, without rolling through all the bytes and producing a hash. The process is as follows.

1. Construct the front feature vector by taking the first N bytes.
2. Look up in the chunk table and collect all entries with a matching front feature vector. For each entry, jump the corresponding distance to check if the end features vectors match.
   1. If the feature vectors match, that indicates a duplicate chunk has probably been found;
   2. otherwise, the chunk is considered unique, and we skip forward the minimum chunk length and the remainder of the chunk is processed following regular CDC.
3. When the chunk boundary is found for a unique chunk, insert its feature vectors and length into the metadata table.

Dynamically Adjusting Mask Bits

QuickCDC’s approach to adjusting the mask bits appears to be identical to the normalized chunking introduced in the FastCDC paper [3]. However, QuickCDC applies this strategy to Rabin chunking, rather than the Gear chunking used in FastCDC.

And so what remains to be seen after the QuickCDC paper [2] is whether using Gear-based chunking will result in an greater speedup than the Rabin variant of QuickCDC. That could be an interesting avenue for experimentation, and is also called out as a point of future research in the paper.

Word of Caution

Now it could just be that I’ve missed reading these sections in the papers, but neither one appears to mention a scenario where the chunk’s length stays the same despite bytes in the middle of the chunk being changed.

Let’s take QuickCDC for example. Consider the scenario where the front and end feature vectors match, and the chunk length matches, but some data was changed in the middle of the chunk. What happens then?

Well, all the paper says is that “there is a certain error ratio” which seems to indicate that data would be lost. So perhaps QuickCDC is not ideal for use cases where data durability is critical, such as building a backup system.

Similarly for RapidCDC, this case might slip through depending on the criteria used for accepting chunk size hints. And all the paper says on this is “it may cause a loss of deduplication opportunities”.

But if you’re building a backup system, where every bit needs to be stored faithfully, then this seems like a pretty bad outcome of using either of these two algorithms.

One approach to guard against data loss in this way is to fallback to cryptographic hashing. In QuickCDC for example, we know for certain if a chunk is unique, but we only know probabilistically if a chunk is a duplicate. So in the later case, we can hash the chunk’s contents to confirm if we have a duplicate, or if some bytes in the middle have changed.

This would introduce a significant performance penalty, and feels like it counteracts the benefits we get from the skipping techniques in RapidCDC and QuickCDC. With an approach like this, chunking does require reading every byte in the data stream.

Wrapping Up

It’s hard to say exactly how much faster QuickCDC is than FastCDC. And the inference of how much fast RapidCDC is than FastCDC is just that, an inference. Though it seems clear that the skipping techniques introduced do make CDC much faster, if also less durable with respect to the data stream.

It’s an interesting problem to consider folding part of these skipping techniques into FastCDC, while avoiding the issue where the middle of the chunk is changed. But that can be a problem for future me to ponder.

Until then, that’s the end of this series. If you’ve read each post of the series, then thank you! And I hope you’ve enjoyed it and found it useful.

There’s a lot about CDC that we haven’t explored. How Rabin chunking works, multi-threaded implementations, improving performance with GPU acceleration, and many other chunking algorithms. But those will have to wait for a future series.

References

1. RapidCDC: Leveraging Duplicate Locality to Accelerate Chunking in CDC-based Deduplication Systems. Ni, F., & Jiang, S. (2019)
2. QuickCDC: A Quick Content-Defined Chunking Algorithm Based on Jumping and Dynamically Adjusting Mask Bits. Xu, Z., & Zhang, W. (2021)
3. FastCDC: A Fast and Efficient Content-Defined Chunking Approach for Data Deduplication. Wen X., et al. (2016)